The observed maximal gaps between prime triplets near p are at most log p times the average gap.
The approximate size of a maximal gap that ends at p is given by the following empirical formula:
whereE(max g3(p)) = a(log(p/a) − 2/3) = O(log4p)
Maximal gaps between prime triplets of each type are listed below.
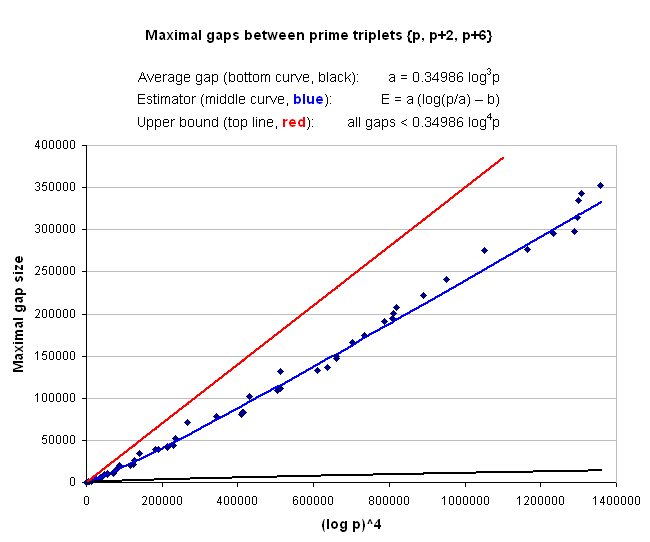
Maximal gaps between prime triplets {p, p+2, p+6}
1st triplet: 2nd triplet: Gap g3(p):
5 11 6
17 41 24
41 101 60
107 191 84
347 461 114
461 641 180
881 1091 210
1607 1871 264
2267 2657 390
2687 3251 564
6197 6827 630
6827 7877 1050
39227 40427 1200
46181 47711 1530
56891 58907 2016
83267 86111 2844
167621 171047 3426
375251 379007 3756
381527 385391 3864
549161 553097 3936
741677 745751 4074
805031 809141 4110
931571 937661 6090
2095361 2103611 8250
2428451 2437691 9240
4769111 4778381 9270
4938287 4948631 10344
12300641 12311147 10506
12652457 12663191 10734
13430171 13441091 10920
14094797 14107727 12930
18074027 18089231 15204
29480651 29500841 20190
107379731 107400017 20286
138778301 138799517 21216
156377861 156403607 25746
242419361 242454281 34920
913183487 913222307 38820
1139296721 1139336111 39390
2146630637 2146672391 41754
2188525331 2188568351 43020
3207540881 3207585191 44310
3577586921 3577639421 52500
7274246711 7274318057 71346
33115389407 33115467521 78114
97128744521 97128825371 80850
99216417017 99216500057 83040
103205810327 103205893751 83424
133645751381 133645853711 102330
373845384527 373845494147 109620
412647825677 412647937127 111450
413307596957 413307728921 131964
1368748574441 1368748707197 132756
1862944563707 1862944700711 137004
2368150202501 2368150349687 147186
2370801522107 2370801671081 148974
3710432509181 3710432675231 166050
5235737405807 5235737580317 174510
8615518909601 8615519100521 190920
10423696470287 10423696665227 194940
10660256412977 10660256613551 200574
11602981439237 11602981647011 207774
21824373608561 21824373830087 221526
36385356561077 36385356802337 241260
81232357111331 81232357386611 275280
186584419495421 186584419772321 276900
297164678680151 297164678975621 295470
428204300934581 428204301233081 298500
450907041535541 450907041850547 315006
464151342563471 464151342898121 334650
484860391301771 484860391645037 343266
666901733009921 666901733361947 352026
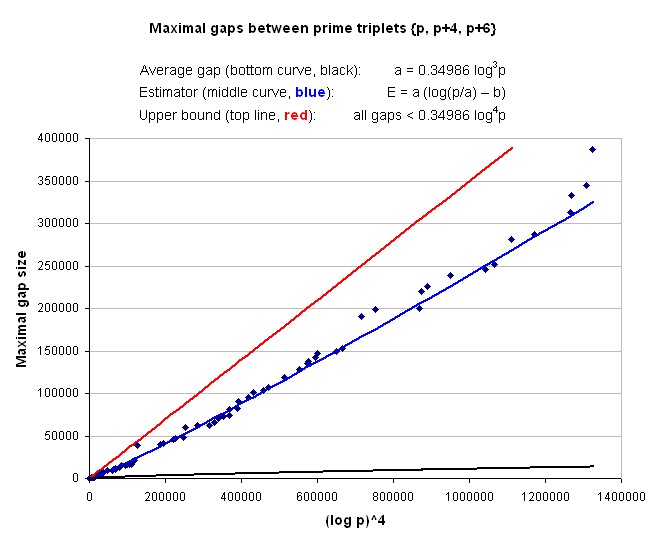
Maximal gaps between prime triplets {p, p+4, p+6}
1st triplet: 2nd triplet: Gap g3(p):
7 13 6
13 37 24
37 67 30
103 193 90
307 457 150
457 613 156
613 823 210
2137 2377 240
2377 2683 306
2797 3163 366
3463 3847 384
4783 5227 444
5737 6547 810
9433 10267 834
14557 15643 1086
24103 25303 1200
45817 47143 1326
52177 54493 2316
126487 130363 3876
317587 321817 4230
580687 585037 4350
715873 724117 8244
2719663 2728543 8880
6227563 6237013 9450
8114857 8125543 10686
10085623 10096573 10950
10137493 10149277 11784
18773137 18785953 12816
21297553 21311107 13554
25291363 25306867 15504
43472497 43488073 15576
52645423 52661677 16254
69718147 69734653 16506
80002627 80019223 16596
89776327 89795773 19446
90338953 90358897 19944
109060027 109081543 21516
148770907 148809247 38340
1060162843 1060202833 39990
1327914037 1327955593 41556
2562574867 2562620653 45786
2985876133 2985923323 47190
4760009587 4760057833 48246
5557217797 5557277653 59856
10481744677 10481806897 62220
19587414277 19587476563 62286
25302582667 25302648457 65790
30944120407 30944191387 70980
37638900283 37638972667 72384
49356265723 49356340387 74664
49428907933 49428989167 81234
70192637737 70192720303 82566
74734558567 74734648657 90090
111228311647 111228407113 95466
134100150127 134100250717 100590
195126585733 195126688957 103224
239527477753 239527584553 106800
415890988417 415891106857 118440
688823669533 688823797237 127704
906056631937 906056767327 135390
926175746857 926175884923 138066
1157745737047 1157745878893 141846
1208782895053 1208783041927 146874
2124064384483 2124064533817 149334
2543551885573 2543552039053 153480
4321372168453 4321372359523 191070
6136808604343 6136808803753 199410
18292411110217 18292411310077 199860
19057076066317 19057076286553 220236
21794613251773 21794613477097 225324
35806145634613 35806145873077 238464
75359307977293 75359308223467 246174
89903831167897 89903831419687 251790
125428917151957 125428917432697 280740
194629563521143 194629563808363 287220
367947033766573 367947034079923 313350
376957618687747 376957619020813 333066
483633763994653 483633764339287 344634
539785800105313 539785800491887 386574
The ratio g3(p)/log4p is never greater than 0.35, i.e.
maximal gap sizes are less than log p times the average gap, where p is the prime at the end of the gap.
Copyright © 2011-2013, Alexei Kourbatov, JavaScripter.net.