Maximal gaps between prime septuplets

Prime septuplets (7-tuples) are the densest permissible clusters of 7 consecutive primes. There are two types of prime septuplets:

{p, p+2, p+6, p+8, p+12, p+18, p+20} (OEIS A022009, A201051, A201249, A233425)

{p, p+2, p+8, p+12, p+14, p+18, p+20} (OEIS A022010, A201251, A201252, A233038).

The observed maximal gaps between prime septuplets near p are at most log p times the average gap.
The approximate size of a maximal gap that ends at p is given by the following empirical formula:

E(max g₇(p)) = a(log(p/a) − 2/7) = O(log⁸p)

where a = 0.018528 log⁷p is the average gap, as predicted by the Hardy-Littlewood k-tuple conjecture.

Maximal gaps between prime septuplets of each type are listed below.

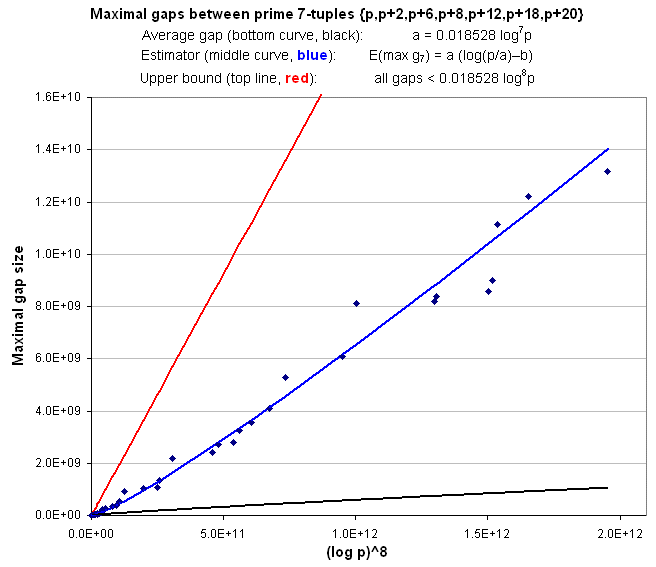
Maximal gaps between prime septuplets {p, p+2, p+6, p+8, p+12, p+18, p+20}

 1st septuplet:  2nd septuplet:   Gap g₇(p): 
             11           165701       165690
         165701          1068701       903000
        1068701         11900501     10831800
       25658441         39431921     13773480
       45002591         67816361     22813770
       93625991        124716071     31090080
      257016491        300768311     43751820
      367438061        428319371     60881310
      575226131        661972301     86746170
     1228244651       1346761511    118516860
     1459270271       1699221521    239951250
     2923666841       3205239881    281573040
    10180589591      10540522241    359932650
    15821203241      16206106991    384903750
    23393094071      23911479071    518385000
    37846533071      38749334621    902801550
   158303571521     159330579041   1027007520
   350060308511     351146640191   1086331680
   382631592641     383960791211   1329198570
   711854781551     714031248641   2176467090
  2879574595811    2881987944371   2413348560
  3379186846151    3381911721101   2724874950
  5102247756491    5105053487531   2805731040
  5987254671311    5990491102691   3236431380
  7853481899561    7857040317011   3558417450
 11824063534091   11828142800471   4079266380
 16348094430581   16353374758991   5280328410
 44226969237161   44233058406611   6089169450
 54763336591961   54771443197181   8106605220
154325181803321  154333374270191   8192466870
157436722520921  157445120715341   8398194420
281057032201481  281065611322031   8579120550
294887168565161  294896169845351   9001280190
309902902299701  309914040972071  11138672370
419341934631071  419354153220461  12218589390
854077393259801  854090557643621  13164383820

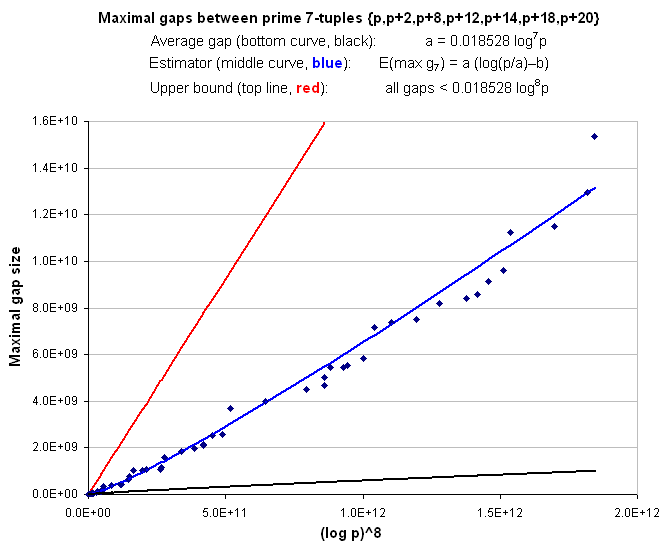
Maximal gaps between prime septuplets {p, p+2, p+8, p+12, p+14, p+18, p+20}

 1st septuplet:  2nd septuplet:   Gap g₇(p): 
           5639           88799        83160
          88799          284729       195930
         284729          626609       341880
        1146779         6560999      5414220
        8573429        17843459      9270030
       24001709        42981929     18980220
       43534019        69156539     25622520
       87988709       124066079     36077370
      157131419       208729049     51597630
      522911099       615095849     92184750
      706620359       832143449    125523090
     1590008669      1730416139    140407470
     2346221399      2488117769    141896370
     3357195209      3693221669    336026460
    11768282159     12171651629    403369470
    30717348029     31152738299    435390270
    33788417009     34230869579    442452570
    62923039169     63550891499    627852330
    68673910169     69428293379    754383210
    88850237459     89858819579   1008582120
   163288980299    164310445289   1021464990
   196782371699    197856064319   1073692620
   421204876439    422293025249   1088148810
   427478111309    428623448159   1145336850
   487635377219    489203880029   1568502810
   994838839439    996670266659   1831427220
  1554893017199   1556874482069   1981464870
  2088869793539   2090982626639   2112833100
  2104286376329   2106411289049   2124912720
  2704298257469   2706823007879   2524750410
  3550904257709   3553467600029   2563342320
  4438966968419   4442670730019   3703761600
  9996858589169  10000866474869   4007885700
 21937527068909  21942038052029   4510983120
 29984058230039  29988742571309   4684341270
 30136375346249  30141383681399   5008335150
 32779504324739  32784963061379   5458736640
 40372176609629  40377635870639   5459261010
 42762127106969  42767665407989   5538301020
 54620176867169  54626029928999   5853061830
 63358011407219  63365153990639   7142583420
 79763188368959  79770583970249   7395601290
109974651670769 109982176374599   7524703830
145568747217989 145576919193689   8171975700
196317277557209 196325706400709   8428843500
221953318490999 221961886287509   8567796510
249376874266769 249385995968099   9121701330
290608782523049 290618408585369   9626062320
310213774327979 310225023265889  11248937910
471088826892779 471100312066829  11485174050
631565753063879 631578724265759  12971201880
665514714418439 665530090367279  15375948840

The ratio g₇(p)/log⁸p is never greater than 0.018528, i.e. maximal gap sizes are less than log p times the average gap, where p is the prime at the end of the gap.